Bayesian Optimization Exploration

Posted on August 26, 2016

A short exploration of using bayesian optimization to make a good choice of hyperparameters. The detailed jupyter notebook can be found in RegressionWithBayesOpt.ipynb.

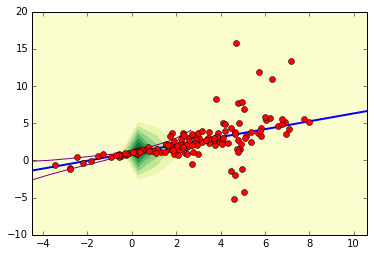
Consider the following data set (pictured at two separate scales):

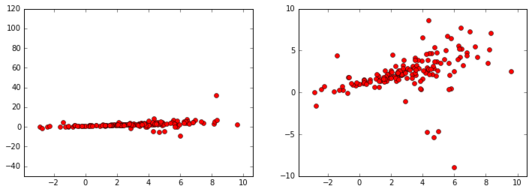
Scatter Plot of Data
Scatter Plot of Data

There seems to be a linear relationship between \(x\) and \(y\), and the \(y\)-values seem to concentrate near \(x=0\) and disperse for large values of \(x\). We want to model the data near \(x=0\) via the following model

\[y=ax+b+\epsilon\]

where \(\epsilon\) is noise which depends on \(x\). Notice that there are some extreme outliers, so using a least-squares approach doesn’t lead to a good fit:

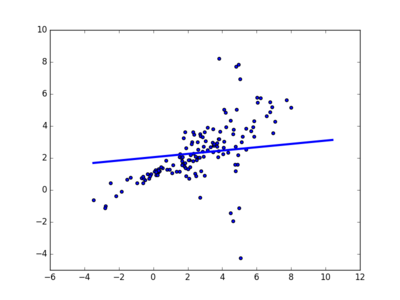
Unregularized Fit
Unregularized Fit

We need \(\epsilon\) to heavy-tailed; so we fit a student t distribution (where the mode, scale, and shape all depend on \(x\)) using gradient descent.

Of course, this is a toy problem, which we are playing with because it is simple to visualize; this exploration is really about Bayesian optimization: The challenge is that we won’t acheive a good fit without proper regularization, and we then need to choose hyperparameters \(\lambda_1,\dots,\lambda_n\) to control the regularization. For any given choice of hyperparameters, we can fit our model on a training subset of the data, and then evaluate the fit on a cross-validation subset of data leading to an error function:

\[\varepsilon_{CV}(\lambda_1,\dots,\lambda_n):=\textrm{CrossValidationError}(\lambda_1,\dots,\lambda_n)\]

which we want to minimize. To minimize this we could use:

  1. A grid search for optimal values of \(\lambda_1,\dots,\lambda_n\),
  2. A random search for optimal values of \(\lambda_1,\dots,\lambda_n\),
  3. Numerical Optimization (such as Nelder-Mead),
  4. Bayesian Optimization.

Note that sampling \(\varepsilon_{CV}\) at a choice of hyperparameters can be costly (since we need to fit our model each time we sample); so rather than sampling \(\varepsilon_{CV}\) either randomly or on a grid, we’d like to make informed decisions about the best places at whcih to sample \(\varepsilon_{CV}\). Numerical Optimization and Bayesian Optimization both attempt to make these informed decisions, and we focus on Bayesian Optimization in this tutorial.

The basic idea is as follows: we will sample \(\varepsilon_{CV}\) at a relatively small number of points, and then fit a gaussian process to that sample: i.e. we model the function \(\varepsilon_{CV}(\lambda_1,\dots,\lambda_n)\) (pictured in red):

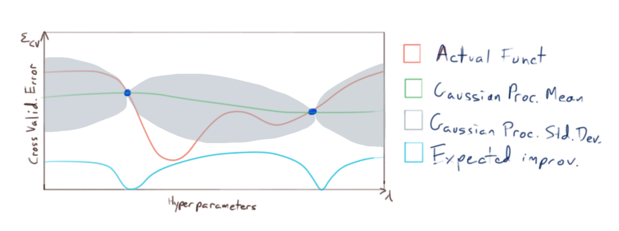
Gaussian Process fit to two samples
Gaussian Process fit to two samples

This model give us estimates of both

  1. the expected (mean) value of \(\varepsilon_{CV}\) if we were to sample it at novel points (pictured in green), as well as
  2. our uncertainty (or expected deviation) from that mean (the region pictured in grey),

and we use this information to choose where to sample \(\varepsilon_{CV}\) next. Now it is important to note that our primary concern is not to accurately model \(\varepsilon_{CV}\) everywhere with our gaussian process; our primary concern is to accurately model \(\varepsilon_{CV}\) near it’s minimums. So we sample \(\varepsilon_{CV}\) at points where we have the greatest expected improvement of fitting our model to the minimums of \(\varepsilon_{CV}\):

Gaussian Process fit to three samples
Gaussian Process fit to three samples

and we repeat until our model fits \(\varepsilon_{CV}\) accurately enough near it’s minimums:

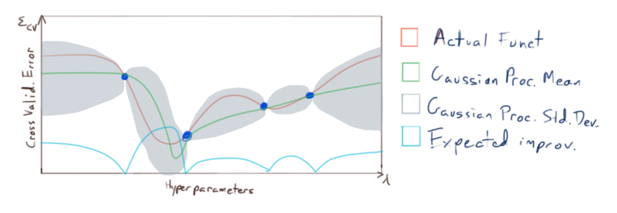
Gaussian Process fit to four samples
Gaussian Process fit to four samples

Finally, we use the resulting model to make an optimal choice for our hyperparameters \(\lambda_1,\dots,\lambda_n\).

This leads to a much better fit (green is the probability density, purple is one standard deviation - only when defined):

regularized_fit
regularized_fit

The full tutorial (with lots of comments and details) can be found in the jupyter notebook RegressionWithBayesOpt.ipynb.